Tak zwane karne schematy pozwalają utrzymać kontakt (’contact’) poprzez dodanie sprężyny w punktach przenikania. Choć jest to bardzo proste do wykonania, to ma kilka poważnych wad. Na przykład, trudno jest wybrać odpowiednią stałą skokową w taki sposób, aby z jednej strony, obiekty nie przenikały się za bardzo, a z drugiej – wynikowy system nie był niestabilny. W innych systemach symulacji fizyki, kolizje są obsługiwane poprzez przewijanie czasu (na przykład przez wyszukiwanie binarne) do dokładnego punktu zderzenia, stamtąd analityczną obsługę kolizji, a następnie ponowne uruchomienie symulacji – nie jest to bardzo praktyczne z punktu widzenia czasu rzeczywistego, ponieważ kod może potencjalnie działać bardzo powoli, gdy istnieje wiele kolizji.

Tutaj wykorzystamy jeszcze inną strategię. Kłopotliwe punkty są po prostu rzutowane na przeszkody. Jako rzutowanie, mamy na myśli przesunięcie punktu w jak najmniejszym stopniu, dopóki jest wolny od przeszkód. Zwykle oznacza to przeniesienie punktu prostopadle w kierunku zderzenia z powierzchnią.

Sprawdźmy to na przykładzie. Załóżmy, że nasz świat znajduje się wewnątrz kostki (0,0,0) – (1000,1000,1000) i przyjmijmy, że współczynnik restytucji cząstek wynosi zero (czyli cząstki nie odbijają się od powierzchni podczas kolizji). Aby utrzymać wszystkie pozycje w poprawnych granicach, odpowiedni kod będzie wyglądał następująco:

(vmax działa na wektorach biorąc maksymalną wartość z obu składników, a vmin – minimalną). Dzięki temu wszystkie cząstki są trzymane wewnątrz sześcianu i obsługiwane są zarówno kolizje jak i 'resting contact’. Piękno w systemie całkowania Verleta polega na tym, że odpowiednie zmiany w prędkościach będą przetwarzane automatycznie. W kolejnych wywołaniach funkcji TimeStep() prędkość jest automatycznie regulowana, aby nie zawierała składnika w kierunku normalnym do powierzchni (odpowiada to zerowemu współczynnikowi restytucji). Patrz rys. 1.

Wypróbuj go – nie ma potrzeby bezpośrednio anulować prędkości w kierunku normalnym. Choć może wydawać się to nieco trywialne, gdy spogląda się na cząstki, siła algorytmu całkowania Verleta powoli się ujawnia i zaczyna być naprawdę widoczna po wprowadzeniu ograniczeń (ograniczników) i połączeniu sztywnych ciał.

Rozwiązywanie kilku jednoczesnych ograniczeń przy użyciu metody relaksacyjnej

Wspólny wzorzec materiału składa się z prostego systemu wzajemnie połączonych sprężyn i cząsteczek. Jednak nie zawsze sprawą prostą jest rozwiązanie odpowiedniego systemu równań różniczkowych. Cierpi on na niektóre z problemów, z jakimi borykają się systemy oparte na karze (penalty-based systems): silne sprężyny powodują sztywność (stiff) systemów równań, które prowadzą z kolei do niestabilności, jeśli tylko proste techniki całkowania są stosowane, lub co najmniej do złej wydajności – co bywa bolączką. Natomiast słabe sprężyny prowadzą do elastycznie wyglądającego materiału.

Jednak dzieje się ciekawa rzecz, gdy pozwolimy sztywności sprężyny przejść do nieskończoności: system nagle staje się rozwiązywalny w sposób stabilny z bardzo prostym i szybkim podejściem. Ale zanim będziemy nadal rozmawiać o materiałach, ponownie zajmijmy się poprzednim przykładem. Sześcian rozważany wcześniej jako zbiór jednostronnych (nierówności) ograniczeń (po jednym dla każdej strony kostki) na pozycjach cząstki, które powinny być spełnione w każdym czasie:

(C1)

W przykładzie, ograniczenia zostały spełnione (czyli cząstki są przechowywane wewnątrz kostki) poprzez prostą modyfikację pozycji przez rzutowanie cząsteczek na powierzchnię kostki. Aby zaspokoić (C1), skorzystamy z następującego pseudo-kodu

Można myśleć o tym procesie, jako o wkładaniu nieskończenie sztywnej sprężyny między cząstki oraz przenikania przez powierzchnię – sprężyny są tak silne i odpowiednio amortyzowane, że od razu będą osiągać ich pozostałą długość zerową (rest length zero).

Rozszerzymy teraz eksperyment, aby zamodelować pręt o długości 100. Robimy to poprzez utworzenie dwóch pojedynczych cząstek (w pozycjach oraz ) i nałożenie warunku, aby znajdowały się w odległości 100 od siebie. Otrzymujemy więc matematycznie następujące obustronne (równanie) ograniczenie:

(C2)

Mimo, że cząstki mogą być początkowo prawidłowo rozmieszczone, po jednym kroku całkowania dystans między nimi mógłby stać się niewłaściwy. W celu ponownego uzyskania prawidłowej odległości będziemy poruszać cząsteczkami przez projekcje ich na zestaw rozwiązań opisanych w (C2). Odbywa się to przez odsunięcie cząstek bezpośrednio od siebie lub przyciągnięcie ich do siebie (w zależności od tego, czy odległość jest zbyt mała lub zbyt duża). Patrz rys. 2.

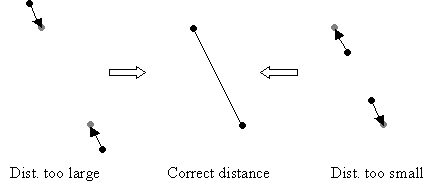
Pseudo-kod spełniający ograniczenia (C2):

Należy pamiętać, że 'delta’ jest wektorem, tak więc delta * delta jest w rzeczywistości iloczynem skalarnym. Przyjmując restlength = 100, powyższy pseudo-kod rozdzieli lub połączy cząsteczki w taki sposób, by ponownie zachować poprawną odległość 100 między nimi. Znów można tu myśleć o sytuacji, gdy bardzo sztywna sprężyna o długości 100 została włożona między cząstki w taki sposób, że są one natychmiast prawidłowo rozmieszczane.

Teraz zakładamy, że cząsteczki nadal spełniają ograniczenia kostki. Przez trzymanie się ograniczeń, możemy jednak unieważnić jedno lub więcej ograniczeń kostki wyciskając z niej cząstki. Taka sytuacja może być niezwłocznie naprawiona przez projekcję wypadającej cząstki z powrotem na powierzchnię kostki – ale wtedy z kolei nie spełniamy ograniczeń.

To, co powinniśmy zrobić, to znaleźć rozwiązanie dla wszystkich ograniczeń naraz, zarówno (C1) i (C2). Byłaby to kwestia systemu rozwiązania równań. Jednak wolimy postępować pośrednio poprzez lokalne iteracje. Po prostu powtarzamy dwie części pseudo-kodu kilka razy po sobie w nadziei, że wynik będzie przydatny. To daje następujący kod:

(inicjalizacja dwóch cząsteczek została pominięta.) Choć te zwykłe iteracje mogą wydawać się nieco naiwne, okazuje się, że prowadzą faktycznie do rozwiązania, którego szukamy! Jest to metoda relaksacyjna (lub Jacobiego lub Gaussa-Seidela w zależności od tego, jak w jaki sposób liczymy (patrz [((bibcite Press))])). Działa ona przez kolejno spełniane różne lokalne ograniczenia, a następnie powtórzenie; jeśli warunki są spełnione, to układ będzie dążyć do globalnej konfiguracji, która spełnia wszystkie ograniczenia w tym samym czasie. Jest to przydatne w wielu innych sytuacjach, gdy wiele współzależnych ograniczeń musi być spełnionych jednocześnie.

Liczba niezbędnych powtórzeń różni się w zależności od symulowanego systemu i liczby ruchów. Może zostać przystosowana poprzez pomiar zmian od ostatniej iteracji. Jeśli wcześnie zatrzymamy iteracje, wynik może nie być do końca poprawny, ale ze względu na zastosowany algorytm Verleta, w kolejnej klatce będzie prawdopodobnie lepszy, w następnej jeszcze bardziej itd. Oznacza to, że wczesne zatrzymanie nie zrujnuje wszystkiego, chociaż wynikowa animacja może nie wydawać się zadowalająca.

Symulacja materiałów

Z faktu, że pręt ograniczeń może być traktowany jako naprawdę twarda sprężyna powinna wynikać jego użyteczność dla symulacji materiału jako zarys na początku tej sekcji. Załóżmy na przykład, że została skonstruowana sześciokątna siatka trójkątów opisująca materiał. Dla każdego wierzchołka inicjalizowana jest cząstka i dla każdego brzegu inicjalizowany jest pręt ograniczeń między dwoma odpowiadającymi cząstkami (z ograniczeniem 'rest length’ jako początkowa odległość między dwoma wierzchołkami).

Funkcja HandleConstraints() używa następnie metody relaksacyjnej przy wszystkich ograniczeniach. Pętla relaksacyjna może być powtórzona kilka razy. Jednakże w celu uzyskania ładnej animacji, dla większości kawałków materiału tak naprawdę tylko jedna iteracja jest konieczna! Oznacza to, że czas symulacji materiału zależy głównie od N operacji kwadratowych i N dzieleń (gdzie N oznacza liczbę krawędzi w siatce materiału). Jak zobaczymy, sprytny trik pozwala zmniejszyć tę liczbę do N dzieleń na klatę – to naprawdę szybko i można by argumentować, że prawdopodobnie nie można uzyskać tego szybciej.

Mamy teraz do omówienia, w jaki sposób pozbyć się pierwiastka kwadratowego. Jeżeli spełnione są wszystkie ograniczenia, już wiemy, że wynik operacji pierwiastkowania w szczegółowym ograniczeniu wyrażenia powinien być pozostałą długością r odpowiedniego pręta. Możemy użyć tego faktu do przybliżenia pierwiastka kwadratowego funkcji. Matematycznie, to, co robimy, jest przybliżeniem funkcji kwadratowej przez jej rozwinięcie I rzędu w szereg Taylora w otoczeniu reszty kwadratowej r*r (odpowiada to pojedynczej iteracji Newtona-Raphsona z pierwotną wartością r). Po drobnym przepisaniu otrzymujemy następujący pseudo-kod:

Zauważ, że jeśli odległość jest już poprawna (tzn. jeśli |delta| = restlength), wtedy przyjmowana jest delta = (0,0,0) i nie zachodzi żadna zmiana.

Na każde ograniczenie wykorzystujemy teraz zero pierwiastków kwadratowych, tylko jedno dzielenie, i może być już nawet policzona wcześniej wartość kwadratowa restlength*restlength! Ilość czasochłonnych operacji zostaje teraz zmniejszona od N dzieleń na klatkę (oraz odpowiadający im dostęp do pamięci) – nie można zrobić tego szybciej i nawet rezultat jest całkiem okazały. Faktycznie, w Hitmanie, ogólna szybkość symulacji materiału była ograniczona głównie przez tyle trójkątów, ile to było możliwe do przeprowadzenia renderowania.

Spełnienie ograniczeń nie jest zagwarantowane po przeprowadzeniu tylko jednej iteracji, jednak dzięki całkowaniu Verleta system będzie szybciej zbliżał się do prawidłowego stanu w kolejnych klatkach. W rzeczywistości, używając tylko jednej iteracji i aproksymując pierwiastek kwadratowy usuwa się sztywność, która pojawia się, gdy pręty są doskonale sztywne.

Umieszczając pomocnicze pręty między strategicznie wybranej pary wierzchołków dzielące sąsiada, algorytm dla materiału może zostać rozszerzony do symulacji roślin. Znowu, w Hitmanie tylko jedno przejście przez pętlę relaksacyjną było wystarczające (w rzeczywistości niewielka liczba sprawiała, że rośliny zginały się właściwą ilość razy).

Kod i równania przedstawione w tej sekcji zakładają, że wszystkie cząstki mają jednakowe masy. Oczywiście możliwe jest modelowanie cząstek o różnych masach, równanie tylko trochę bardziej się skomplikuje.

Aby spełnić (C2) przy jednoczesnym wzięciu pod uwagę mas cząstek, użyjemy następującego kodu:

Tutaj invmass1 i invmass2 są odwrotnościami dwóch mas. Jeśli chcemy, aby cząstki były nieruchome, wystarczy ustawić dla nich invmass = 0, (odpowiadające nieskończonej masie). Oczywiście w celu zwiększenia szybkości działania pierwiastek kwadratowy również może być aproksymowany.